Integration
Integration ist der Vorgang zur Berechnung von unbestimmten oder bestimmten Integralen.
Das bestimmte Integral einer Funktion ordnet ihr einen Zahlenwert zu.
Diese Zahl entspricht anschaulich dem Flächeninhalt, der durch den Funktionsgraphen sowie der x-Achse begrenzt wird. Hierbei zählen Flächen unterhalb der x-Achse negativ.
Das unbestimmte Integral einer Funktion ordnet ihr andere Funktionen zu, die Stammfunktion genannt werden. Diese zeichnen sich dadurch aus, dass ihre erste Ableitung die Funktion ist, die integriert wurde.
Der Hauptsatz der Differential- und Integralrechnung besagt, dass bestimmte Integrale mithilfe von Stammfunktionen berechnet werden können.
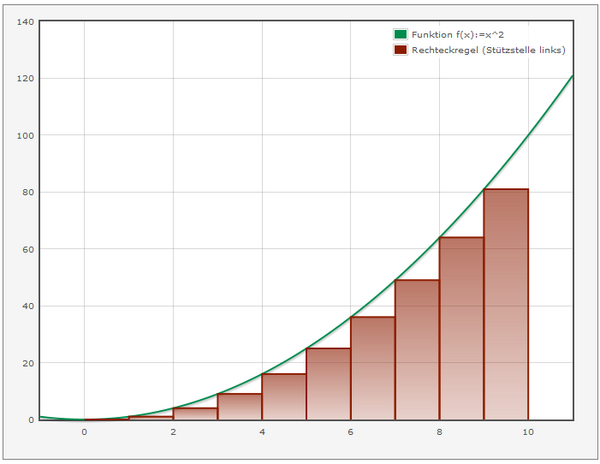
Obwohl man den Eindruck hat, es handelt sich bei der Integration um das Gegenstück zur Differentiation, ist Integration ungemein schwieriger. Um Ableitungen von konkreten Funktionen zu bestimmen, genügt es, wenige definierte Regeln anzuwenden. Zur Integration selbst elementarer Funktionen hingegen existiert kein einfacher und kein alle Fälle abdeckender Algorithmus. Hier ist man viel eher auf numerische Approximationen angewiesen.







