Das Grundmodell der Warteschlangentheorie
Die Warteschlangentheorie bedient sich zur Beschreibung von Bedienungssystemen eines einfachen Grundmodells. Es besteht aus dem sogenannten Bedienungsschalter, der über ein oder mehrere parallel arbeitende gleichartige Maschinen bzw. Arbeitsplätze verfügt, und aus einem Warteraum. Die Kunden treffen einzeln und zu zufälligen Zeitpunkten vor dem Bedienungsgerät ein. Ein neu ankommender Kunde wird bedient, sofern mindestens eines der Bedienungsgeräte frei ist, andernfalls muss er sich in die Warteschlange einreihen.

Das Grundmodell kann auf vielfältige Weise variiert werden:
- Die Kunden werden nicht einzeln, sondern gruppenweise bedient (Wartesysteme mit Gruppenbedienung). Anwendung: Losfertigung in einem Produktionsbetrieb
- Einige Kunden verlassen das System, bevor sie bedient worden sind (Wartesysteme mit Zeitbeschränkungen). Anwendung: Lagerhaltung von verderblicher Ware
- Nicht alle Bedienungsgeräte stehen jedem Kunden zur Verfügung (Bedienungssysteme mit eingeschränkter Erreichbarkeit). Anwendung: Fertigungsstraßen mit dedizierten Maschinen, Koppelanordnungen in einem Fernsprechnetz.
- Einige Kunden scheuen sich, in das Bedienungssystem einzutreten, weil ihnen die Warteschlange zu lang erscheint (Wartesysteme mit ungeduldigen Kunden). Anwendung: übliches Kundenverhalten an einem Post-, Bank- oder Fahrkartenschalter
- Ein Kunde mit höherer Priorität verdrängt einen Kunden niedrigerer Priorität aus dem Bedienungsprozess (Bedienungssysteme mit Prioritätssteuerung). Anwendung: Express-Los-Steuerung in einem Fertigungsprozess
- Ein Kunde, der bei seiner Ankunft nicht sofort bedient werden kann, geht verloren (Verlustsysteme). Anwendung: Telefonate in einem Fernsprechnetz
Der Strom der ankommenden Forderungen wird durch einen sog. Erneuerungsprozess beschrieben. Dazu denken wir uns alle Forderungen in der Reihenfolge ihrer Ankünfte durchnumeriert. Die Zeitspanne In zwischen der Ankunft des (n-1)-ten und des n-ten Kunden wird als Zwischenankunftszeit bezeichnet. Von den Zufallsvariablen In, n = 1, 2, ... wird vorausgesetzt, dass sie stochastisch unabhängig und identisch verteilt sind mit der Verteilungsfunktion Fl(x), dem Erwartungswert E[I] und der Varianz D[I]. Der Kehrwert

heißt Ankunftsrate und gibt an, wieviele Kunden im Durchschnitt pro Zeiteinheit in das System einfallen.
Die Bedienungszeiten Sn, n = 1, 2, ... der aufeinanderfolgenden Kunden werden ebenfalls als stochastisch unabhängige und identisch verteile Zufallsvariablen aufgefasst. Die Verteilungsfunktion der Bedienungszeiten wird mit FS(x) bezeichnet. Für den zugehörigen Erwartungswert und die zugehörige Varianz verwenden wir die Symbole E[S] und D[S]. Der Kehrwert

heißt Bedienrate und gibt an, wieviele Kunden im Durchschnitt pro Zeiteinheit von dem Bedienungssystem abgefertigt werden können. Sind mehrere parallele und gleichartige Bedienungsgeräte vorhanden, erhöht sich die Bedienrate entsprechend der Anzahl der Geräte.
Die Bedienungsregel legt fest, in welcher Reihenfolge die wartenden Kunden abgefertigt werden sollen. Folgende Regeln und Bezeichnungen sind gebräuchlich:
| FIFO (FCFS) | First In, First Out (First Come, First Served). Die Bedienung erfolgt in der Reihenfolge der Ankünfte. | |
| LIFO (LCFS) | Last In, First Out (Last Come, First Served). Die Bedienung erfolgt in umgekehrter Reihenfolge der Ankünfte. | |
| SIRO | Selection In Random Order. Der nächste Kunde wird zufällig ausgewählt. | |
| Non-preemptive priority | Relative Priorität. Manche Kunden werden gegenüber anderen Kunden vorrangig behandelt. Der laufende Bedienungsprozess wird jedoch nicht unterbrochen. | |
| Preemptive priority | Absolute Priorität. Besitzt der neu ankommende Kunde gegenüber den anderen Kunden im System eine höhere Priorität, so wird der laufende Bedienungsprozess unterbrochen und mit der neuen Forderung fortgesetzt. Die alte Forderung wird zurückgestellt. | |
| RR | Round Robin. Jeder Kunde kann den Bediener jeweils nur für ein bestimmtes Zeitintervall in Anspruch nehmen. Kunden, deren Abfertigung mehr Zeit benötigt, müssen sich deshalb mehrmals hintereinander in die Warteschlange einreihen. |
Zur symbolischen Kennzeichnung von Bedienungssystemen haben D.G. Kendall und B.W. Gnedenko die Notation
A / B / c /m
eingeführt. Die Buchstaben A und B markieren hierbei den Verteilungstyp der Zwischenankunftszeiten und der Bedienungszeiten. Der Buchstabe c steht für die Anzahl der parallelen Bediener und m bezeichnet die Kapazität des Warteraums.
Für den Verteilungstyp sind folgende Abkürzungen gebräuchlich:
| D | Deterministische Verteilung |
| M | Exponentialverteilung |
| Ek | Erlang-Verteilung mit Parameter k (k = 1, 2, ...) |
| Hk | Hyperexponentialverteilung mit Parameter k (k = 1, 2, ...) |
| PH | Phasentyp-Verteilung |
| G | Allgemeine Verteilung |
Beispiel: Die Notation M/G/3/5 kennzeichnet ein Bedienungsystem mit exponentialverteilten Zwischenankunftszeiten, beliebig verteilten Bedienzeiten, drei parallelen Bedienern und einem Warteraum, in dem maximal 5 Kunden warten können.
Die Leistungsbewertung von Bedienungssystemen erfolgt auf der Basis folgender Prozesse:
- Anzahl Kunden im System (Nt)t>0. Dieser Prozess gibt an, wieviele Kunden sich zur Zeit t im Bedienungssystem aufhalten.
- Der Prozess der aufeinanderfolgenden Verweilzeiten (bzw. Durchlaufzeiten)(Vn)n in N. Die Zufallsvariable Vnbezeichnet die Zeit, die der n-te Kunde im Bedienungssystem verweilt
Zur Berechnung der Kenngrößen können verschiedene Methoden der Theorie der Stochastischen Prozesse herangezogen werden. Die Eignung einer Methode hängt sehr stark davon ab, welche Verteilungstypen für die Zwischenankunfts- und Bedienungszeiten zugrundegelegt werden und ob zeitabhängige oder stationäre Größen berechnet werden sollen. Schon das Grundmodell der Warteschlangentheorie ist so kompliziert, dass es unter allgemeinen Verteilungsannahmen nicht exakt gelöst werden kann. Es existieren allerdings Näherungsformeln, die sich in der Praxis recht gut bewährt haben und die die stochastische Funktionsweise von Bedienungssystemen transparent machen. Nach einer Formel von Allen-Cunnen gilt für die mittlere Anzahl Kunden im stationären Fall:

Hierbei bedeuten ρ die Auslastung des Systems, Wurzel(ρc+1) die Wartewahrscheinlichkeit und cI2 sowie cS2 die Variationskoeffizienten der Zwischenankunfts- und Bedienungszeiten. Die Formel lehrt uns, dass die Anzahl Kunden im System umso größer ist, je größer die Auslastung des Systems und die Variationskoeffizienten sind. Um eine geringe Warteschlange zu bekommen, muss man folglich genügend Kapazität bereitstellen oder die Variabilität des Systems gering halten.
Die Mittlere Verweilzeit erhält man mit Hilfe der Formel von Little:

wobei λ die Inputrate des Systems bedeutet.
Ausgehend von den Formeln lassen sich folgende Zusammenhänge veranschaulichen:
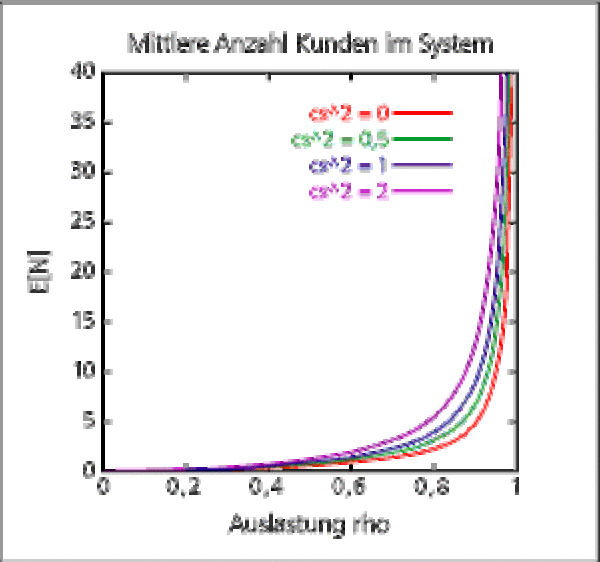
Die mittlere Anzahl Kunden im System hängt von der Auslastung der Bedienstation ab. Mit wachsender Auslastung ρ wächst auch die Anzahl Kunden im System. Außerdem beobachtet man: Je größer der Variationskoeffizient der Bedienzeit ist, umso größer ist auch die mittlere Anzahl Kunden im System E[N].

Die mittlere Verweilzeit E[V] ist offensichtlich mit der mittleren Anzahl Kunden im System korreliert. Je größer die Auslastung und die Variabilität des Systems, desto länger muß gewartet werden.
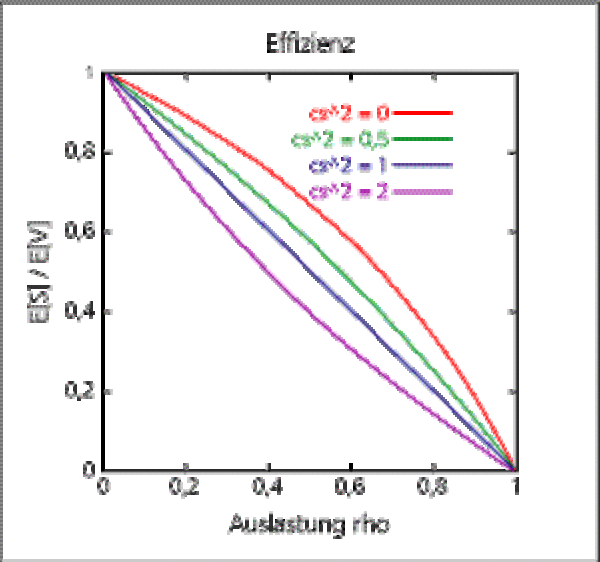
Als Effizienz bezeichnet man das Verhältnis von reiner Bedienzeit zur gesamten Verweilzeit eines Kunden. Da die Verweilzeit mit zunehmender Auslastung über alle Grenzen wächst, strebt die Effizienz gegen Null.

Unsere Formel erlaubt auch, den Auslastungsgrad ρ in Abhängigkeit vom Umlaufbestand E[N] darzustellen. Der Graph zeigt, das man ab einem gewissen Auslastungsgrad trotz höherer Bestände keinen höheren Durchsatz erzielt. Deswegen sollten z. B. in der Produktion erst dann wieder neue Aufträge eingelastet werden, wenn der Bestand unter eine kritische Grenze gesunken ist (sogenannte belastungorientierte Auftragsfreigabe).




